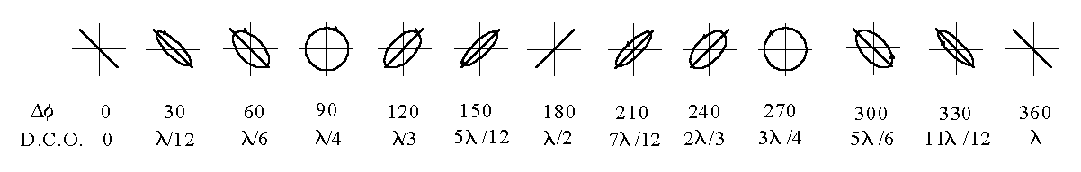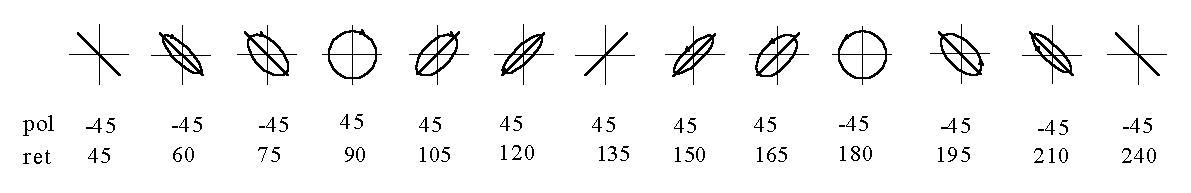
U A B C
Facultad de Ciencias
Carrera de Física
Laboratorio de Óptica, otoño 2002
Prof. Roberto Machorro
Práctica 4
Polarización de la luz
Versión 5 octubre 2002, RMM

|
U A B C Facultad de Ciencias Carrera de Física Laboratorio de Óptica, otoño 2002 Prof. Roberto Machorro |
Práctica 4 Polarización de la luz Versión 5 octubre 2002, RMM |
|
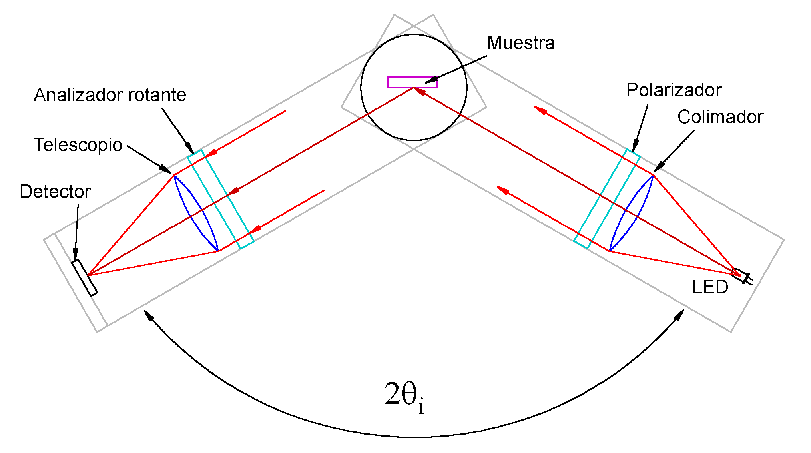
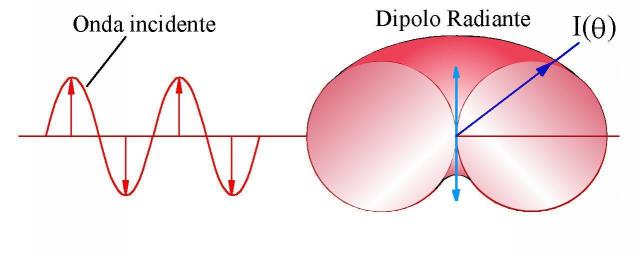
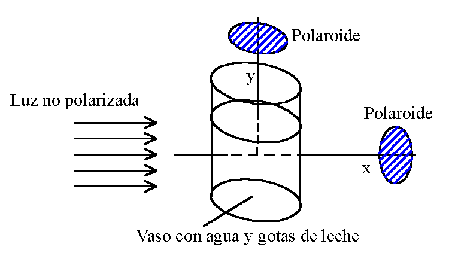
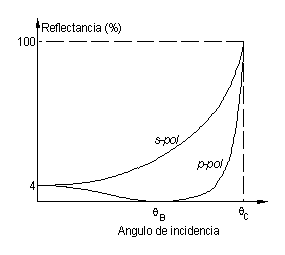
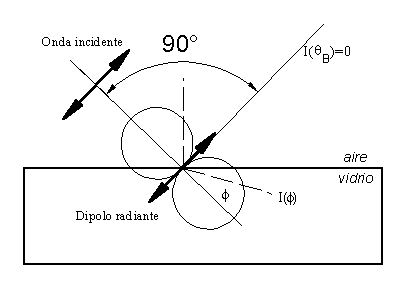
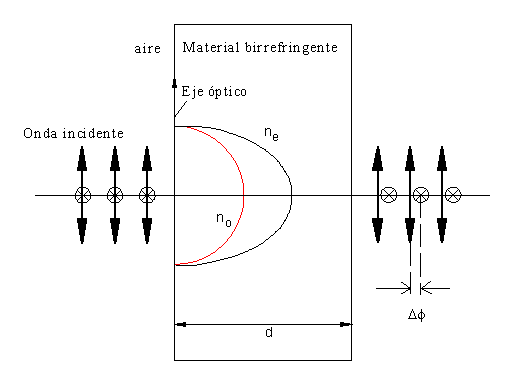
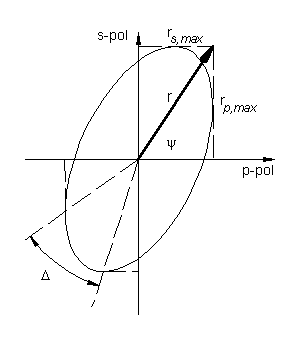
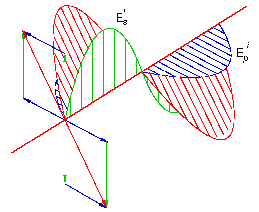
Objetivos Metodología: Semana No. 1, Dicroismo. Ley de Malus Metodología: Semana No. 2, Dispersión de luz. Birrefringencia Metodología: Semana No. 3, Reflexión de luz Produciendo luz con polarización controlada Elipsometría Reporte de la práctica Plan semanal y Material de laboratorio |
Ir a menú de Prácticas de Óptica |